Diberikan dua buah fungsi distribusi probabilitas diskrit $P(x)$ dan $Q(x)$, bagaimana cara mengukur kedekatan diantara kedua fungsi tersebut? Salah satu alat ukur yang populer digunakan adalah Kullback-Leibler (KL) divergence:
\[\begin{equation}
\label{eq:kl}
\displaystyle \mathrm{KL}( P \| Q) = \sum_x P(x) \log \frac{ P(x) }{ Q(x) }
\end{equation}\]
Fungsi divergensi di atas dapat diartikan sebagai kedekatan fungsi probabilitas $Q$ menuju $P$.
KL Divergence memenuhi sifat positif-definit:
- \(\displaystyle \mathrm{KL}(P \| Q) \geq 0\),
- \(\displaystyle \mathrm{KL}(P \| Q) = 0 \iff P=Q\),
namun tidak simetris \(\mathrm{KL}(P \| Q) \neq \mathrm{KL}( Q \| P)\).
Oleh karena itu, \(\mathrm{KL}(\cdot \| \cdot)\) disebut sebagai fungsi divergensi, bukan fungsi jarak – fungsi jarak harus memenuhi kedua sifat positif-definit dan simetris.
Fungsi KL pertama kali ini diperkenalkan oleh Solomon Kullback dan Richard Leibler pada tahun 1951, yang akhirnya menjadi kuantitas sangat penting pada teori informasi.
KL seringkali digunakan untuk melakukan optimisasi yang melibatkan distribusi probabilitas pada banyak aplikasi seperti mekanika fluida, neurosains, dan machine learning (terutama pada Bayesian inference).
Tulisan ini membahas Kullback-Leibler Divergence dari prinsip-prinsip utamanya, yaitu teori probabilitas dan teori informasi.
Eksperimen, Hasil Eksperimen, Ruang Sampel, Kejadian, Variabel Acak, dan Probabilitas
Judul sub-bab ini menunjukkan elemen-elemen dasar dari teori probabilitas.
Kita definisikan element-element tersebut sebagai berikut.
- Eksperimen: Sebuah prosedur yang dapat dilakukan berulang kali dan memiliki hasil keluaran.
- Hasil eksperimen (outcome): Keluaran dari eksperimen.
- Ruang sample (\(\Omega\)): Himpunan dari semua hasil eksperimen yang mungkin terjadi.
$$ \
- Kejadian (\(E\)): himpunan dari sebagian hasil eksperimen, i.e., \(E \subseteq \Omega\).
- Variabel acak (\(X: \Omega \rightarrow \mathbb{R}\)): fungsi yang memberikan sebuah nilai atau label terhadap hasil eksperimen.
- Probabilitas (\(P: E \rightarrow [0, 1]\)): fungsi yang memberikan nilai hanya antara 0 hingga 1 terhadap suatu kejadian yang memiliki arti seberapa pasti kejadian tersebut terjadi.
Salah satu contoh dari eksperimen adalah melempar dadu sebanyak 2 kali.
Hasil dari eksperimen ada 36 kemungkinan yang dapat dinyatakan dengan ruang sampel \(\Omega = \{ (1, 1), (1, 2), \ldots, (6, 5), (6, 6) \}\) dimana masing-masing anggotanya merupakan hasil eksperimen.
Contoh dari kejadian dari eksperimen tersebut adalah hasil eksperimen dimana terdapat elemen \(x\) pada lemparan pertama, \(E_x = \{ (x, 1), \ldots, (x, 6) \}\).
Kita dapat mengasosiasikan tiap hasil eksperimen dengan variabel acak.
Misalnya, tiap elemen \((x, 1), (x, 2), \ldots, (x, 6)\) kita beri label \(x, \forall x = 1, \ldots, 6\).
Untuk \(x = 1\) kita dapat tulis dengan notasi variabel acak \(X( (1, 1) ) = 1, X( (1, 2)) = 1, \ldots, X(1, 6) = 1\), dan seterusnya.
Perlu diperhatikan bahwa penentuan variabel acak sangat bergantung dengan konteks, namun pada prinsipnya bertujuan untuk mengelompokkan hasil eksperimen menjadi sebuah kejadian.
Sekarang kita hitung probabilitas dari kejadian
\(E_x = \{ \omega \in \Omega | X(\omega) = x\}\).
\[\begin{eqnarray}
P( \{ \omega \in \Omega | X(\omega) = x\} ) &=& \frac{ \text{jumlah anggota himpunan } E_x }{\text{jumlah angota himpunan } \Omega} \nonumber \\
&=& \frac{6}{36} = \frac{1}{6} \nonumber
\end{eqnarray}\]
Untuk kenyamanan biasanya notasi
\(P( \{ \omega \in \Omega | X(\omega) = x \} )\)
kita singkat menjadi
\(P(X = x)\) atau
\(P(x)\).
Distribusi probabilitas
Distribusi probabilitas merupakan fungsi yang memberikan nilai kepastian / ketidakpastian terhadap seluruh kejadian dari suatu eksperimen.
Ini merupakan kasus khusus dari fungsi probabilitas yang telah kita definisikan sebelumnya.
Fungsi probabilitas \(P(X = x)\) dikatakan sebagai distribusi probabilitas apabila memenuhi persyaratan:
- Bernilai antara 0 hingga 1: \(\displaystyle P(X = x) \in [0, 1]\).
- Berjumlah total 1 terhadap seluruh kejadian: \(\displaystyle \sum_x P(X = x) = 1\).
Misalkan suatu eksperimen hanya memiliki 2 kejadian yang diwakili dengan variabel acak \(X = 1\) dan \(X = 2\),
- Jika \(P(X = 1) = 0.3\) dan \(P(X = 2) = 0.7\), maka fungsi \(P(X = x)\) merupakan distribusi probabilitas.
- Jika \(P(X = 1) = 0.3\) dan \(P(X = 2) = 0.9\), maka fungsi \(P(X = x)\) bukan merupakan distribusi probabilitas, karena \(\sum_x P(X = x) > 1\).
Penggunaan sehari-hari kata “informasi” biasanya identik dengan sesuatu yang memiliki makna. Namun pada bidang teori informasi, informasi dikaji secara kuantitatif – makna semantik dari informasi itu sendiri di luar aspek teori informasi.
Bagaimana mengkuantifikasi informasi? Definisi matematis yang disepakati berkaitan erat dengan probabilitas.
Secara matematis, informasi merupakan fungsi skor \(I_P: \mathcal{X} \rightarrow \mathbb{R}\), dimana $\mathcal{X}$ merupakan variabel acak. Misalkan ada sebuah kejadian $x$ dengan probabilitas $P(x)$, nilai informasi dari kejadian $x$ didefinisikan sebagai negatif dari log probabilitas
\[\begin{equation}
\displaystyle I_P(x) = - \log P(x).
\end{equation}\]
Definisi di atas mengindikasikan bahwa semakin besar probabilitas dari suatu kejadian, semakin kecil nilai informasinya, begitu pula sebaliknya (perhatikan Gambar 1).
Interpretasi lain namun serupa yaitu semakin tidak pasti suatu kejadian maka semakin tinggi nilai informasinya – oleh karena itu, istilah lain dari \(I_P(x)\) adalah surprisal (kejutan).
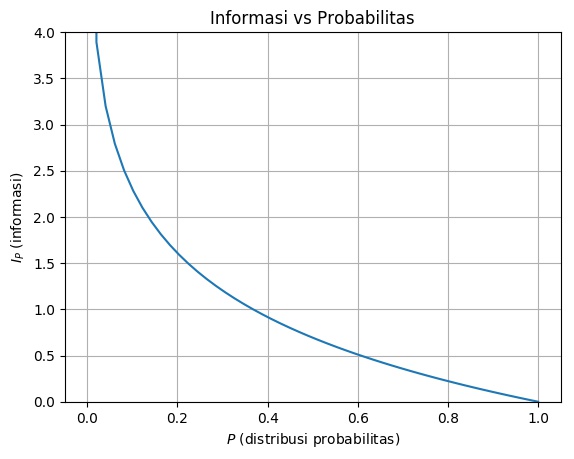
Gambar 1. Informasi vs Probabilitas
Jika dipikir lebih lanjut, pengertian di atas cukup intuitif. Perhatikan contoh pernyataan berikut ini:
Pada tahun 2030 Indonesia menjadi negara maju
Tanpa bermaksud pesimis, unsur ketidakpastian pernyataan tersebut masih ada.
Artikel di sini membahas tentang prediksi Indonesia menjadi negara maju dari segi pertumbuhan ekonomi, namun membahas pula peluang kegagalan untuk maju.
Jika pengertian “maju” di sini diperluas lagi dengan menggunakan ukuran Human Development Index yang juga mencakup unsur pendidikan, harapan hidup, dan lain-lain, maka akan menjadi semakin sulit diprediksi.
Kalimat berikut ini pun sama atau mungkin lebih tidak pasti lagi:
Indonesia akan bubar pada tahun 2030.
Ini hanya sekadar contoh bahwa dibutuhkan informasi tambahan untuk menaikan level kepastian pernyataan di atas. Dengan kata lain, nilai informasinya tinggi.
Coba bandingkan dengan pernyataan di bawah ini:
Semua pedagang kaki lima, kakinya cuma dua.
– Cak Lontong –
Karena memang hampir pasti pedagang kaki lima (manusia) punya 2 kaki, nilai informasinya rendah. Bahkan frasa “kakinya cuma dua” tidak begitu penting untuk disebut.
Entropi
Fungsi $I_P(x)$ memberikan nilai informasi terhadap 1 kejadian $x$.
Jumlah kejadian bisa ada banyak.
Dapatkah kita mengukur nilai informasi beberapa kejadian dengan 1 alat ukur?
Cara yang paling mudah adalah dengan menghitung rata-rata / ekspektasi dari informasi.
Misalkan terdapat variabel acak dengan $n$ buah kejadian \(X = \{ x_1, \ldots, x_n \}\) dengan probabilitas $P(x_i)$, ekspektasi dari informasi $I_P(x)$ dapat dinyatakan dalam fungsi sebagai berikut:
\[\begin{equation}
H_P(X) = \sum_{x \in X} P(x) I_P(x) = - \sum_{x \in X} P(x) \log P(x)
\end{equation}\]
Fungsi di atas populer dengan nama Shannon entropy (Shannon 1948).
Istilah entropy juga dikenal pada bidang termodinamika yang mengukur derajat kekacauan dari kumpulan partikel.
Jadi secara intuitif serupa dengan Shannon entropy: rata-rata ketidakpastian / kejutan.
Contoh sederhana penggunaan entropi adalah mengukur ketidakpastian hasil kejadian melempar uang logam/koin.
Ambil katakanlah koin Rp500 yang memiliki 2 sisi: “Melati” (M) dan “Garuda” (G) lalu kita tulis dengan variabel acak \(X = \{ M, G\}\).
Anggaplah ini koin yang adil / memiliki nilai probabilitas yang sama: \(P(M) = P(G) = 0.5\).
Entropi dari kejadian lempar koin adalah sebagai berikut:
\[\begin{eqnarray}
H_P(X) &=& - \sum_{x \in \{ M, G\}} P(x) \log P(x) \nonumber \\
&=&- P(M) \log P(M) - P(G) \log P(G) \nonumber \\
&=& - 0.5 \log_2 0.5 - 0.5 \log_2 0.5 \nonumber \\
&\approx& 0.69 \nonumber
\end{eqnarray}\]
Bandingkan dengan kejadian melempar dadu yang memiliki 6 sisi \(X = \{ s_1, s_2, s_3, s_4, s_5, s_6\}\), masing-masing memiliki probabilitas \(P(s_1) = \ldots = P(s_6) = \frac{1}{6}\).
Kita akan mendapatkan angka entropi sebesar \(H_P(X) \approx 1.79\) (silakan dicek ulang).
Dari contoh sederhana ini kita dapat menyimpulkan bahwa kejadian melempar dadu (6 kemungkinan kejadian) memiliki rata-rata ketidakpastian / surprisal yang lebih tinggi dibandingkan melempar koin.
Contoh lain, bagaimana nilai entropi atau derajat kekacauan dari kumpulan berita hoax? Dapat dipastikan sangat tinggi!
Lintas-Entropi
Penghitungan entropi di atas menggunakan distribusi probabilitas yang sama, \(P(x)\), baik untuk mengukur informasi maupun nilai rata-rata/ekspektasi. Dan fungsi probabilitas \(P\) berasosiasi langsung dengan variabel random \(X\), dimana kerjadian-kejadian \(x_1, \ldots, x_n \in X\) merupakan sampel dari \(P\).
Kita dapat mengukur nilai informasi dengan menggunakan fungsi probabilitas yang tidak terasosiasi dengan suatu sampel.
Lebih jelasnya, misalkan terdapat sampel \(x \in X\) yang terasosiasi dengan fungsi probabilitas \(P\) dan fungsi probabilitas lain bernama \(Q\), kita dapat menghitung informasi dalam bentuk:
\[\begin{equation}
I_Q(x) = - \log Q(x) \nonumber
\end{equation}\]
Jika kita hitung ekspektasi dari \(I_Q\) terhadap distribusi probabilitas \(P\), maka kita akan mendapatkan bentuk entropi lain yang disebut sebagai lintas-entropi (cross-entropy):
\[\begin{eqnarray}
H_{[P,Q]}(X) &=& \sum_{x \in X} P(x) I_Q(x) \nonumber \\
&=& - \sum_{x \in X} P(x) \log Q(x)
\end{eqnarray}\]
Di sini kita memiliki 2 buah fungsi probabilitas, yaitu \(P(x)\) dan \(Q(x)\).
Ingat kembali bahwa distribusi probabilitas \(P(x)\) merupakan sumber dari himpunan sampel \(X = \{x_1, \ldots, x_n \}\).
Pada kasus tertentu, kita tidak mengetahui fungsi probabilitas \(P(x)\) namun hanya dapat mengakses data atau sampelnya.
Salah satu kegunaan lintas-entropi adalah untuk mengestimasi fungsi \(P(x)\) yang tidak diketahui, melalui fungsi \(Q(x)\) dari data/sampel yang kita asumsikan berasal dari $P(x)$.
Ini merupakan problem aproksimasi fungsi yang lazim ditemukan pada optimisasi dan machine learning.
Diketahui $n$ buah sampel yang bersumber dari distribusi \(P\), yaitu \(x_1, \ldots, x_n \sim P\), pilih sebuah fungsi distribusi probabilitas estimasi \(Q(x)\) yang kita ketahui bentuknya, misalnya distribusi normal
\[\begin{eqnarray}
\displaystyle
Q(x) = \mathcal{N}(x | \mu, \sigma) =
\frac{1}{ \sqrt{2 \pi \sigma^2 }} \exp \left(- \frac{(x - \mu)^2}{2 \sigma^2} \right)
\end{eqnarray}\]
Lalu kita “paksa” fungsi probabilitas \(Q\) supaya mirip-mirip dengan \(P\) dengan cara meminimumkan lintas-entropi empiris sebagai berikut:
\[\begin{eqnarray}
\label{eq:opt_h}
Q^* := \arg \min_{Q} \left[ H_{[P, Q]} = - \frac{1}{n} \sum_{i=1}^n \log Q(x_i) \right]
\end{eqnarray}\]
Jika $n$ berjumlah besar, \(Q^*\), yang masih berbentuk distribusi normal, akan dekat dengan \(P\).
Jadi, kita dapat melihat bahwa lintas-entropi dapat digunakan untuk membandingkan 2 buah fungsi probabilitas \(P\) dan \(Q\): nilainya semakin kecil apabila kedua fungsi tersebut saling mendekat.
Bagaimana jika fungsi probabilitas \(P\) dan \(Q\) identik?
Secara intuitif kita membutuhkan alat ukur yang mengembalikan nilai 0 untuk 2 benda yang sama.
Namun demikian, lintas-entropi tidak memberikan nilai 0 untuk \(P = Q\) (dapat pula dicek bahwa lintas-entropi tereduksi entropi untuk \(P = Q\)).
Berikut ini contoh yang mendukung pernyataan tersebut.
Misalkan \(P\) dan \(Q\) merupakan distribusi probabilitas yang hanya memiliki 2 kemungkinan outcome \(\mathcal{X} = \{ 1, 2\}\):
\[P(x) = Q(x) =
\begin{cases}
0.9 & \quad \text{jika } x = 1 \\
0.1 & \quad \text{jika } x = 2
\end{cases}\]
Dengan demikian, lintas-entropi dari \(P\) dan \(Q\)
\[\begin{equation}
H_{[P, Q]} = H_{[P, P]} = - 0.9 \log{0.9} - 0.1 \log{0.1} \approx 0.33 > 0 \nonumber
\end{equation}\]
\(H_{[P, P]}\) akan memberikan nilai yang berbeda pula untuk bentuk fungsi \(P\) yang berbeda (tidak selalu 0.33).
Kullback-Leibler Divergence
Kullback-Leibler Divergence \(\mathrm{KL}(P \| Q)\) memiliki makna yang analog dengan lintas-entropi, yaitu mengukur kedekatan antar 2 distribusi probabilitas, lihat kembali persamaan (\(\ref{eq:kl}\)).
Namun fungsi \(\mathrm{KL}\) mengatasi permasalahan yang ada pada lintas-entropi, yaitu memiliki karakteristik \(\mathrm{KL}(P \| Q) = 0\) untuk \(P = Q\).
\[\begin{eqnarray}
\mathrm{KL}( P \| P) &=& \sum_x P(x) \log \frac{ P(x) }{ P(x) }
&=& \sum_x P(x) \log 1
&=& 0
\end{eqnarray}\]
Oleh karena itu, kita akan mengetahui dengan pasti bahwa \(P\) persis sama atau tidak dengan \(Q\) (apapun bentuk dari \(P\) dan \(Q\)) dengan mengecek nilai \(\mathrm{KL} (P \| Q)\).
Kita juga dapat menyatakan problem optimisasi seperti pada (\(\ref{eq:opt_h}\)) dengan menggunakan \(\mathrm{KL}\):
\[\begin{equation}
\label{eq:opt_kl}
Q^* := \arg \min_{Q} \mathrm{KL}( P || Q)
\end{equation}\]
Apabila optimisasi dilakukan secara iteratif, keuntungan optimisasi (\(\ref{eq:opt_kl}\)) dibandingkan (\(\ref{eq:opt_h}\)) adalah kita mengetahui persis kapan optimisasi tersebut harus berhenti, yaitu pada titik \(\mathrm{KL}(P \| Q^*) = 0\).
Bagaimana hubungan antara Kullback-Leibler Divergence, Entropi, dan Lintas-Entropi?
Dengan aljabar sederhana di bawah ini, kita akan melihatnya dengan jelas:
\[\begin{eqnarray}
\mathrm{KL}( P \| Q) &=& \sum_x P(x) \log \frac{P(x)}{Q(x)} \nonumber \\
&=& - \sum_x P(x) \log \frac{ Q(x) }{ P(x) } \nonumber \\
&=& - \sum_x P(x) \left ( \log Q(x) - \log P(x) \right) \nonumber \\
&=& - \sum_x P(x) \log Q(x) + \sum_x P(x) \log P(x) \nonumber \\
&=& H_{[P, Q]} - H_{P} \nonumber
\end{eqnarray}\]
Jadi, ternyata KL = lintas-entropi - entropi, yang membuat Kullback-Leibler Divergence dikenal pula dengan istilah entropi relatif.
Kesimpulan
Berikut beberapa poin penting dari tulisan ini:
- Teori informasi berkaitan erat dengan probabilitas: informasi dikuantifikasi dengan fungsi probabilitas yang mengukur derajat ketidakpastiaan / kejutan / kekacauan dari suatu kejadian.
- Entropi merupakan ukuran rata-rata derajat ketidakpastiaan dari seluruh kejadian yang ada pada suatu eksperimen.
- Lintas-entropi dan Kullback-Leibler Divergence merupakan ekstensi dari entropi yang dapat digunakan untuk mengukur kedekatan dari 2 distribusi probabilitas.
- Kullback-Leibler Divergence memiliki karakteristik yang tidak dimiliki lintas-entropi: bernilai 0 apabila 2 buah fungsi probabilitas \(P\) dan \(Q\) identik.