Rigid body merupakan sebuah objek geometris terdiri dari kumpulan titik yang membentuk suatu struktur benda solid, i.e.,
tidak terjadi deformasi pada benda tersebut. Kumpulan titik merah pada Gambar 1 mengilustrasikan sebuah rigid body.
Sebagaimana halnya objek geometris, kita dapat mengaplikasikan berbagai transformasi geometris pada rigid body seperti translasi, rotasi, dan dilasi.
Kumpulan titik biru pada Gambar 1 merupakan hasil rotasi rigid body berwarna merah.
Sebuah rigid body dengan \(m\) buah titik di ruang 3D dapat kita tulis dalam notasi matriks sebagai berikut:
\[\begin{align}
\mathbf{P} =
\begin{bmatrix}
| & | & \cdots & | \\
\mathbf{p}_1 & \mathbf{p}_2 & \cdots & \mathbf{p}_m \\
| & | & \cdots & |
\end{bmatrix} \in \mathbb{R}^{3 \times m} \nonumber,
\end{align}\]
dimana \(\mathbf{p}_i = [x^p_i, y^p_i, z^p_i]^{\top}\) merupakan titik ke-\(i\).
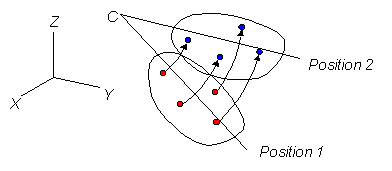
Gambar 1. Rotasi pada rigid body (sumber: www.kwo3d.com/theory/jkinem/rotmat.html)
Pada contoh Gambar 1, \(m=4\).
Misalkan \(\mathbf{Q} \in \mathbb{R}^{3 \times m}\) merupakan sebuah rigid body hasil rotasi dari \(\mathbf{P}\), maka berlaku persamaan:
\[\begin{equation}
\label{eq:rig}
\mathbf{Q} = \mathbf{R} \mathbf{P}
\end{equation}\]
dimana \(\mathbf{R} \in \mathbb{R}^{3 \times 3}\) merupakan matriks rotasi pada ruang 3D:
\[\begin{equation}
\label{eq:rot}
\mathbf{R} =
\underbrace{
\begin{bmatrix}
\cos(\theta_z) & -\sin(\theta_z) & 0 \\
\sin(\theta_z) & \cos(\theta_z) & 0 \\
0 & 0 & 1
\end{bmatrix}
}_{\mathbf{R}_z}
\underbrace{
\begin{bmatrix}
\cos(\theta_y) & 0 & \sin(\theta_y) \\
0 & 1 & 0 \\
-\sin(\theta_y) & 0 & \cos(\theta_y)
\end{bmatrix}
}_{\mathbf{R}_y}
\underbrace{
\begin{bmatrix}
1 & 0 & 0 \\
0 & \cos(\theta_x) & -\sin(\theta_x) \\
0 & \sin(\theta_x) & \cos(\theta_x)
\end{bmatrix}
}_{\mathbf{R}_x}.
\end{equation}\]
Jika \(\mathbf{P}\) dan \(\{ \theta_x, \theta_y, \theta_z \}\) (atau \(\mathbf{R}\)) diketahui, maka \(\mathbf{Q}\) dapat dihitung dengan mudah.
Pada berbagai aplikasi (menghitung spacecraft attitude, menentukan gerakan pada robot, animasi objek-objek grafis, 3D object registration) , kita tertarik untuk mencari matriks rotasi $\mathbf{R}$ diketahui 2 buah rigid body yang saling berkorespondensi.
Korespondensi di sini maksudnya adalah setiap titik pada sebuah rigid body memiliki pasangannya pada rigid body yang lain.
Problem ini dikenal dengan Wahba’s problem atau orthogonal Procrustes problem.
Selanjutnya kita akan membahas bagaimana memecahkan problem ini dengan menggunakan Singular Value Decomposition.
Orthogonal Procrustes Problem
Mencari \(\mathbf{R}\) pada persamaan (\(\ref{eq:rig}\)) tidak cukup mudah dikarenakan matriks \(\mathbf{P} \in \mathbb{R}^{3 \times m}\) tidak dapat di-inverse.
Agar komputasi mungkin dilakukan, kita formulasikan problemnya dalam bentuk minimisasi least square sebagai berikut:
\[\begin{equation}
\label{eq:probls}
\displaystyle
\min_{\mathbf{R} \in \mathbb{R}^{3 \times 3}} \left\{
J(\mathbf{R}) = \left \| \mathbf{Q} - \mathbf{R} \mathbf{P} \right \|_F^2 \right \}
\text{ subject to } \mathbf{R}^{\top} \mathbf{R} = \mathbf{I},
\end{equation}\]
dimana \(\displaystyle \left \| \cdot \right \|_F^2\) merupakan Frobenius norm.
Cara lain untuk mengekspresikan persamaan di atas adalah dengan menggunakan operator trace \(\mathrm{Tr}(\cdot)\):
\[\begin{equation}
\label{eq:probtr}
J(\mathbf{R}) = \mathrm{Tr} \left( (\mathbf{Q} - \mathbf{R} \mathbf{P})^{\top} (\mathbf{Q} - \mathbf{R} \mathbf{P}) \right)
\end{equation}\]
dimana trace melakukan penjumlahan elemen diagonal dari sebuah matriks persegi $\mathbf{A} \in \mathbb{R}^{m \times m}$:
\[\begin{equation}
\mathrm{Tr}(\mathbf{A}) = \sum_{i=1}^m a_{ii} \nonumber
\end{equation}\]
Singular Value Decomposition
Singular Value Decomposition (SVD) merupakan sebuah teknik memecah / dekomposisi / faktorisasi sebuah matriks menjadi 3 buah matriks.
Sebarang matriks \(\mathbf{M} \in \mathbb{R}^{m \times n}\) dapat difaktorisasi menjadi
\[\begin{equation}
\label{eq:svd}
\mathrm{SVD}(\mathbf{M}) = \mathbf{U} \mathbf{\Sigma} \mathbf{V}^{\top}
\end{equation}\]
dimana \(\mathbf{U} \in \mathbb{R}^{m \times m}\) merupakan matriks ortogonal yang dikenal dengan matriks left-singular,
\(\mathbf{\Sigma} \in \mathbb{R}^{m \times n}\) merupakan matriks diagonal dengan elemen non-negatif,
dan \(\mathbf{V} \in \mathbb{R}^{n \times n}\) merupakan matriks ortogonal yang disebut matriks right-singular.
Matriks Rotasi
Secara umum, matriks rotasi pada ruang \(D > 1\) dapat didefinisikan sebagai berikut.
Definisi 1 (Matriks Rotasi).
Sebuah matriks persegi \(\mathbf{R} \in \mathbb{R}^{D \times D}\) merupakan matriks rotasi jika
- \(\mathbf{R}^{-1} = \mathbf{R}^{\top}\), dan
- \(\mathrm{det}(\mathbf{R}) = 1\).
Dapat dicek bahwa matriks $\mathbf{R}$ pada persamaan ($\ref{eq:rot}$) merupakan bentuk khusus untuk dimensi 3 dari definisi di atas.
Solusi
Solusi untuk orthogonal Procrustes problem (\ref{eq:probls}) dikemas dalam teorema berikut ini.
Teorema 1 (Matriks Rotasi).
Diberikan 2 buah rigid body yang berkorespondensi $ \mathbf{X}, \mathbf{Y} \in \mathbb{R}^{3 \times m} $,
dimana vektor-vektor kolom pada kedua matriks tersebut merupakan titik-titik pada ruang 3D.
Jika titik $ \mathbf{c}=(x_c, y_c, z_c) $ merupakan poros rotasi dan matriks $ \mathbf{P}, \mathbf{Q} \in \mathbb{R}^{3 \times m} $ memenuhi
\[\begin{align}
\mathbf{P} &=[\mathbf{p}_1 - \mathbf{c}, \mathbf{p}_2 - \mathbf{c}, \cdots, \mathbf{p}_m - \mathbf{c}], \nonumber \\
\mathbf{Q} &=[\mathbf{q}_1 - \mathbf{c}, \mathbf{q}_2 - \mathbf{c}, \cdots, \mathbf{q}_m - \mathbf{c}], \nonumber
\end{align}\]
maka matriks rotasi \(\mathbf{R}\) yang memberikan solusi untuk problem (\(\ref{eq:probls}\)) dapat dihitung sbb:
\[\begin{align}
\mathbf{R} = \mathbf{V} \mathbf{U}^\top,
\end{align}\]
dimana $ \mathrm{SVD}(\mathbf{P} \mathbf{Q}^\top) = \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^\top $
Bukti. Persamaan (\(\ref{eq:probtr}\)) dapat dijabarkan menjadi
\[\begin{align}
J(\mathbf{R}) &= \mathrm{Tr}\left( (\mathbf{Q} - \mathbf{R} \mathbf{P})^\top(\mathbf{Q} - \mathbf{R} \mathbf{P}) \right) \nonumber \\
&= \mathrm{Tr} \left( \mathbf{Q}^\top \mathbf{Q} - \mathbf{Q}^\top \mathbf{R} \mathbf{P} - \mathbf{P}^\top \mathbf{R}^\top \mathbf{Q} + \mathbf{P}^\top \mathbf{R}^\top \mathbf{R} \mathbf{P} \right) \nonumber \\
& =\mathrm{Tr} \left( \mathbf{Q}^\top \mathbf{Q} - \mathbf{Q}^\top \mathbf{R} \mathbf{P} - \mathbf{P}^\top \mathbf{R}^\top \mathbf{Q} + \mathbf{P}^\top \mathbf{P} \right) \nonumber \\
& =\mathrm{Tr} \left( \mathbf{Q}^\top \mathbf{Q} \right) - 2 \mathrm{Tr} \left( \mathbf{Q}^\top \mathbf{R} \mathbf{P} \right) + \mathrm{Tr}\left( \mathbf{P}^\top \mathbf{P} \right) \nonumber
\end{align}\]
Karena minimisasi \(J(\mathbf{R})\) hanya bergantung pada matriks rotasi \(\mathbf{R}\), kita dapat sederhanakan problem (\(\ref{eq:probls}\)) menjadi
\[\begin{align}
\min_{\mathbf{R}} - \mathrm{Tr}\left( \mathbf{Q}^\top \mathbf{R} \mathbf{P} \right) =- \mathrm{Tr}\left( \mathbf{R} \mathbf{P}\mathbf{Q}^\top \right) \nonumber
\end{align}\]
yang juga dapat ditulis sebagai problem maksimisasi
\[\begin{align}
\max_{\mathbf{R}} \mathrm{Tr}\left( \mathbf{R} \mathbf{P}\mathbf{Q}^\top \right). \nonumber
\end{align}\]
Kemudian kita dekomposisi matriks \(\mathbf{P} \mathbf{Q}^\top\) dengan menggunakan
\(\mathrm{SVD}(\mathbf{P} \mathbf{Q}^\top) = \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^\top\) sehingga menjadi
\[\begin{align}
\label{eq:probmax}
\max_{\mathbf{R}} \mathrm{Tr}\left( \mathbf{R} \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^\top \right) =\max \mathrm{Tr}\left(\boldsymbol{\Sigma} \mathbf{V}^\top \mathbf{R} \mathbf{U} \right).
\end{align}\]
Tulis \(\mathbf{A} = \mathbf{V}^\top \mathbf{R} \mathbf{U}\). Ekspresi di atas mencapai maksimum ketika \(\mathbf{A}= \mathbf{I}\). Dengan demikian,
\[\begin{align}
\mathbf{V}^\top \mathbf{R} \mathbf{U} = \mathbf{I} \nonumber \\
\mathbf{R} = \mathbf{V} \mathbf{U}^\top \nonumber
\end{align}\]
Mungkin ada yang bertanya-tanya mengapa $ \mathbf{A} = \mathbf{I} $ berimplikasi nilai maksimum untuk (\(\ref{eq:probmax}\))? Dengan kata lain, mengapa
$ \displaystyle \max_{\mathbf{R}} \mathrm{Tr}\left( \mathbf{R} \mathbf{U} \boldsymbol{\Sigma} \mathbf{V}^\top \right) = \mathrm{Tr} \left( \mathbf{\Sigma} \right) = \sum_{i=1}^m \sigma_{i} $ ?
Perhatikan bahwa semua matriks yang menyusun $ \mathbf{A} $ merupakan matriks ortogonal, sehingga matriks$ \mathbf{A} $ juga ortogonal.
Dengan demikian, penjumlahan elemen-elemen kolom dari $ \mathbf{A} $ memenuhi $ \displaystyle \sum_{i=1}^m a_{ij}^2 = 1 $, yang berimplikasi $ \displaystyle -1 \leq a_{ij} \leq 1 $.
Maka kita dapat simpulkan bahwa
\[\begin{align}
\mathrm{Tr}\left( \boldsymbol{\Sigma} \mathbf{A} \right) = \sum_{i=1} \sigma_i a_{ii} \leq \sum_{i=1} \sigma_i =
\max \mathrm{Tr}\left( \boldsymbol{\Sigma} \mathbf{A} \right) \nonumber
\end{align}\]
Ilustrasi penggunaan penghitungan rotasi rigid body pada computer graphic dapat dilihat pada video 3D object registration di bawah ini: