Deep learning bekerja melalui proses optimisasi.
Dengan kata lain, artificial neural networks belajar dari data dengan cara mengoptimalkan fungsi objektif.
Dari pertengahan tahun 80-an hingga sekarang, teknik optimisasi yang digunakan berbasis first-order gradient dari fungsi objektif yang disebut sebagai gradient descent (Cauchy, 1847).
Dipadukan dengan chain rule, gradient descent pada neural networks dikenal dengan algoritma back-propagation (Rumelhart et al. 1986).
Di ranah mathematical optimization, gradient descent merupakan metode yang paling sederhana dan telah banyak tersedia metode-metode optimisasi lain yang lebih canggih.
Mengapa deep learning masih mengandalkan gradient descent?
Alasan utamanya adalah skalabilitas komputasi: gradient descent memiliki kompleksitas linear terhadap pertambahan data dan juga mudah untuk dikomputasi secara paralel (dengan memanfaatkan GPU).
Karakteristik ini memungkinkan sebuah model neural network yang cukup besar untuk dilatih dengan jutaan data latih.
Beberapa kisah sukses terkait hal ini antara lain AlexNet (Krizhevsky et al. 2012), Word2Vec (Mikolov et al. 2013), dan ResNet (He et al. 2015).
Misalnya kita punya sebuah neural network \(\displaystyle f_{\boldsymbol{\theta}} : \mathcal{X} \rightarrow \mathcal{Y}\), dimana \(\boldsymbol{\theta}\) merupakan parameter yang nantinya akan disetel berdasarkan data yang dipelajari – pada neural networks parameter ini terdiri dari weights dan bias.
Asumsikan kondisi supervised learning, yaitu \(f_{\boldsymbol{\theta}}\) belajar dari pasangan data \((x, y)\) dan definisikan fungsi loss \(\displaystyle \ell: \mathcal{Y} \times \mathcal{Y} \rightarrow \mathbb{R}\).
Salah satu bentuk fungsi loss, untuk \(\mathcal{Y} \subseteq \mathbb{R}\), adalah least-square error \(L\left(f_{\boldsymbol{\theta}}(x), y \right) = \left( f_{\boldsymbol{\theta}}(x) - y\right)^2\).
Untuk menyederhanakan notasi, tulis \(L(\boldsymbol{\theta}) := L(f_{\boldsymbol{\theta}}(x), y)\).
Tujuan dari optimisasi pada deep learning yaitu meminimalkan fungsi loss
\[\begin{equation}
\label{eq:dlobj}
\min_{\boldsymbol{\theta}} L(\boldsymbol{\theta})
\end{equation}\]
Kita definisikan gradient dari fungsi loss terhadap \(\boldsymbol{\theta}\) dengan notasi
\(\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\).
Gradient Descent (GD)
Kita definisikan gradient dari fungsi loss terhadap \(\boldsymbol{\theta}\) dengan notasi \(\nabla_{\boldsymbol{\theta}} L(\boldsymbol{\theta})\).
Gradient descent melakukan update secara iteratif terhadap parameter \(\boldsymbol{\theta}\) agar objektif (\ref{eq:dlobj}) tercapai
dengan memanfaatkan \(\nabla_{\boldsymbol{\theta}}L(\boldsymbol{\theta})\).
Tahapan GD diringkas pada Algoritma 1.
Algoritma 1 (Gradient Descent).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \textbf{repeat} \\
\text{3: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L( \boldsymbol{\theta}_{t-1}) \\
\text{4: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \mathbf{g}_t \\
\text{5: } \textbf{until}\quad\text{convergence}\)
Gambar 1 mengilustrasikan parameter dengan ruang solusi berdimensi dua – parameter pada neural networks umumnya berdimensi banyak.
Parameter \(\boldsymbol{\theta}\) dapat diilustrasikan sebagai sebuah titik pada ruang solusi.
Secara intuitif, GD memindah-mindahkan titik tersebut berdasarkan arahan dari gradient,
yang menginformasikan jalur tercuram dari suatu posisi tertentu ke posisi tujuan.
Harapannya, akumulasi informasi dari gradient pada tiap-tiap posisi mampu mengantarkan ke solusi optimal.
Gambar 1. Gradient Descent (sumber: http://komarix.org/ac/papers/thesis/thesis_html/img30.png)
Namun demikian, strategi memilih jalur tercuram ini memiliki beberapa kekurangan.
Pertama, terdapat resiko untuk terjebak di solusi yang kurang optimal.
Kedua, tidak ada garansi untuk terjadi konvergensi ke suatu solusi.
Kedua masalah ini terkait juga dengan pemilihan konstanta \(\alpha > 0\) (baris ke-4 pada Algoritma 1).
Jika \(\alpha\) terlalu kecil, maka \(\boldsymbol{\theta}\) berpotensi terperangkap ke local optima,
sedangkan jika terlalu besar maka berpotensi terjadi osilasi/divergensi.
Masalah yang lebih fundamental adalah bahwa mengikuti jalur tercuram belum tentu merupakan cara yang benar atau efisien untuk menuju tujuan solusi,
terutama untuk lanskap ruang solusi yang kompleks.
Bayangkan seseorang yang turun dari perbukitan dengan berjalan kaki, tetapi tidak tahu jalan menuju daratan dan tidak mempunyai peta.
Salah satu metode heuristis yang bisa dipakai adalah selalu mengikuti jalur yang turun ke bawah.
Padahal bisa jadi itu akan membawa kita berputar-putar dahulu sebelum mencapai daratan tujuan, atau bahkan bisa terperangkap ke jurang.
Mungkin saja jalur yang benar adalah dengan cara menaiki bukit-bukit kecil terlebih dahulu, lalu kemudian turun.
Dapatkah GD diperbaiki sehingga mampu membentuk jalur optimisasi yang lebih efisien?
Salah satu cara tradisional untuk melakukan hal tersebut adalah dengan melakukan penjadwalan annealing terhadap learning rate \(\alpha\),
e.g., bernilai besar pada awal iterasi, lalu perlahan-lahan mengecil pada pertengahan / akhir iterasi.
Namun kita memiliki 2 strategi yang lebih elegan: i) momentum dan ii) adaptive subgradient.
GD dengan Classical Momentum (CM)
Momentum (Polyak, 1964) merupakan sebuah metode untuk mengakselerasi GD dengan memanfaatkan informasi gradient dari langkah-langkah sebelumnya.
Akumulasi informasi dari gradient berguna untuk mengurangi efek osilisasi sehingga jalur optimisasi menjadi lebih stabil.
Algoritma 2 di bawah ini merupakan modifikasi dari GD dengan penambahan strategi momentum.
Algoritma 2 (Gradient Descent dengan Classical Momentum (CM)).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \mathbf{m}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1}) \\
\text{5: } \quad \mathbf{m}_t := \mathbf{g}_t + \beta \mathbf{m}_{t-1} \\
\text{6: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \mathbf{m}_t \\
\text{7: } \textbf{until}\quad\text{convergence}\)
Kita sebut saja algoritma ini dengan Classical Momentum (CM) – pada bagian berikutnya akan dibahas metode momentum yang lebih terkini.
Jika dibandingkan dengan GD, CM hanya melakukan satu penambahan, yaitu \(\beta m_{t-1}\),
dimana \(\beta\) merupakan konstanta yang mengatur seberapa besar kontribusi dari gradient sebelumnya.
\(\beta = 0.9\) merupakan best practice dari CM – perhatikan bahwa \(\beta = 0\) akan membuat CM sama persis dengan GD.
Andaikan gradient \(g_t\) merupakan sebuah vektor berdimensi banyak.
Secara intuitif, CM akan memberikan bobot yang lebih pada dimensi tertentu yang memiliki nilai yang konsisten untuk tiap langkah.
Sebaliknya, untuk dimensi yang tidak stabil CM akan memberikan bobot yang lebih kecil.
Hal inilah yang menstabilkan jalur optimisasi dari parameter \(\theta\) sehingga menimbulkan efek akselerasi.
Gambar 2 mengilustrasikan perbedaan antara GD dan CM.
Perbedaan antara GD dan CM juga dapat dijelaskan dengan analogi sebagai berikut: GD seperti seseorang yang berjalan kaki di perbukitan dan mencoba turun ke daratan,
sedangkan CM seperti bola yang menggelinding ke bawah.
Bagi yang tertarik mendalami lebih lanjut tentang CM bisa membaca sebuah tulisan brilian di sini: http://distill.pub/2017/momentum.
Gambar 2. Gradient Descent tanpa Momentum (kiri) vs dengan Momentum (kanan) (sumber: http://sebastianruder.com/optimizing-gradient-descent/)
Nesterov’s Accelerated Gradient (NAG)
Jika kita perhatikan Algoritma 2, CM menghitung vektor gradient \(g_t\) terlebih dahulu, lalu menghitung vektor momentum \(m_t\).
(Sutskever et al. 2013) melakukan look-ahead terhadap vektor parameter \(\theta_t\) dengan menggunakan
momentum sebelum menghitung vektor gradient \(g_t\):
\[g_t = \nabla_{\theta_{t-1}} L(\theta_{t-1} - \beta m_{t-1}).\]
Strategi ini dinamakan dengan Nesterov’s Accelerated Gradient (NAG) ([Nesterov 1983]).
Secara lengkapnya langkah-langkah NAG dapat dilihat pada Algoritma 3.1.
Algoritma 3.1 (Nesterov’s Accelerated Gradient (NAG)).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \mathbf{m}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1} - \beta \mathbf{m}_{t-1}) \\
\text{5: } \quad \mathbf{m}_t := \mathbf{g}_t + \beta \mathbf{m}_{t-1} \\
\text{6: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \mathbf{m}_t \\
\text{7: } \textbf{until}\quad\text{convergence}\)
Perbedaan antara CM dan NAG diilustrasikan pada Gambar 3.
Dapat dilihat bahwa NAG terlebih dahulu ‘memindahkan’ parameter mengikuti vektor momentum, lalu barulah menghitung vektor gradient.
Sedangkan CM menghitung vektor gradient di awal, dan posisi akhir parameter berdasarkan akumulasi antara vektor gradient tersebut dengan vektor momentum.
Walaupun perubahan yang dilakukan nyaris innocent, NAG menghasilkan performa yang lebih baik dibandingkan CM baik secara empiris maupun dari sisi teori.
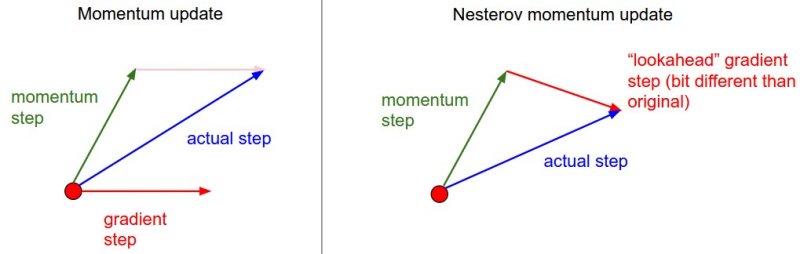Gambar 3. Classical Momentum vs Nesterov’s Accelerated Gradient (sumber: http://cs231n.github.io/assets/nn3/nesterov.jpeg)
Untuk kemudahan implementasi, kita dapat menulis ulang algoritma NAG seperti pada Algoritma 3.2.
Algoritma 3.2 (Nesterov’s Accelerated Gradient (NAG)).
\(\text{1: } \theta_0 = \mathrm{rand()} \\
\text{2: } \mathbf{m}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1}) \\
\text{5: } \quad \mathbf{m}_t := \mathbf{g}_t + \beta \mathbf{m}_{t-1} \\
\text{6: } \quad \hat{\mathbf{m}}_t := \mathbf{g}_t + \beta \mathbf{m}_t \\
\text{7: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \hat{\mathbf{m}}_t \\
\text{8: } \textbf{until}\quad\text{convergence}\)
AdaGrad dan RMSProp
Cara lain untuk memperbaiki GD selain dengan momentum adalah dengan memberikan kecepatan update yang berbeda pada tiap dimensi vektor parameter \(\theta_t\) dan mampu beradaptasi berdasarkan indikator tertentu.
Salah satu indikator yang dapat dipakai adalah besarnya perubahan nilai vektor gradient pada dimensi tertentu.
Realisasi dari ide ini dikenal dengan metode adaptive subgradient descent (AdaGrad) (Duchi et al. 2011), yang diringkas pada Algoritma 4 di bawah ini.
Algoritma 4 (AdaGrad).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \mathbf{n}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1}) \\
\text{5: } \quad \mathbf{n}_t := \mathbf{g}^2_t + \mathbf{n}_{t-1} \\
\text{6: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \frac{\mathbf{g}_t}{ \sqrt{\mathbf{n}_t} + \varepsilon} \\
\text{7: } \textbf{until}\quad\text{convergence}\)
Perhatikan bahwa \(\sqrt{\mathbf{n}_t}\) memberikan informasi seberapa besar perubahan nilai sebuah elemen pada vektor gradient, yang berfungsi sebagai faktor skala untuk gradient \(\mathbf{g}_t\) – operasi pembagian pada baris 6 merupakan operasi per-elemen antar 2 vektor.
Apabila nilai \(\sqrt{\mathbf{n}_t}\) pada dimensi tertentu mengecil, maka kecepatan update pada dimensi tersebut bertambah, dan sebaliknya.
Hal ini akan menyeimbangkan kontribusi dari tiap dimensi dari vektor gradient sehingga membuat jalur optimisasi menjadi lebih stabil.
AdaGrad memiliki sebuah problem, yaitu pada waktu tertentu nilai \(\mathbf{n}_t\) berpotensi sangat besar sehingga malah akan memperlambat proses optimisasi.
Untuk mengatasi hal ini, (Tieleman dan Hinton 2012)
melakukan sedikit modifikasi terhadap AdaGrad dengan menambahkan konstanta \(\gamma\) dan \(1-\gamma\) untuk mengatur besaran masing-masing dari
\(\mathbf{g}^2_t\) dan \(\mathbf{n}_t\).
Modifikasi ini menghasilkan nama algoritma baru yang disebut dengan RMSProp – bandingkan baris ke-5 pada Algoritma 4 dan 5.
Algoritma 5 (RMSProp).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \mathbf{n}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1}) \\
\text{5: } \quad \mathbf{n}_t := (1 - \gamma) \mathbf{g}^2_t + \gamma \mathbf{n}_{t-1} \\
\text{6: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \frac{\mathbf{g}_t}{ \sqrt{\mathbf{n}_t} + \varepsilon} \\
\text{7: } \textbf{until}\quad\text{convergence}\)
Adam
Kita telah melihat bahwa terdapat 2 pendekatan yang berbeda untuk memperbaiki gradient descent: i) momentum dan ii) adaptive subgradient.
Dapatkah kita menggabungkan keduanya sehingga dapat memanfaatkan hal yang terbaik dari kedua pendekatan tersebut?
(Kingma and Ba 2015) menjawab pertanyaan ini dengan mengkombinasikan RMSProp dan classical momentum (CM).
Algoritma baru yang dihasilkan bernama adaptive moment estimation (Adam).
Algoritma 6 (Adam).
\(\text{1: } \boldsymbol{\theta}_0 = \mathrm{rand()} \\
\text{2: } \mathbf{n}_0 = 0 \\
\text{3: } \textbf{repeat} \\
\text{4: } \quad \mathbf{g}_t := \nabla_{\boldsymbol{\theta}_{t-1}} L(\boldsymbol{\theta}_{t-1}) \\
\text{5: } \quad \mathbf{m}_t := (1 - \beta) \mathbf{g}_t + \beta \mathbf{m}_{t-1} \\
\text{6: } \quad \hat{\mathbf{m}}_t := \frac{\mathbf{m}_t}{1 - \beta^t} \\
\text{7: } \quad \mathbf{n}_t := (1 - \gamma) \mathbf{g}^2_t + \gamma \mathbf{n}_{t-1} \\
\text{8: } \quad \hat{\mathbf{n}}_t := \frac{\mathbf{n}_t}{1 - \gamma^t} \\
\text{9: } \quad \boldsymbol{\theta}_t := \boldsymbol{\theta}_{t-1} - \alpha \frac{\hat{\mathbf{m}}_t}{ \sqrt{\hat{\mathbf{n}}_t} + \varepsilon} \\
\text{10: } \textbf{until}\quad\text{convergence}\)
Dapat kita lihat pada Algoritma 6, baris ke-5 merupakan unsur momentum dan baris ke-7 merupakan unsur adaptive subgradient.
Adam juga menggunakan teknik bias correction yang memberikan aproksimasi lebih baik untuk \(\mathbf{m}_t\) dan \(\mathbf{n}_t\).
Saat ini Adam menjadi pilihan favorit sebagai alat optimisasi pada deep learning.