Salah satu problem klasik pada Computer Vision adalah bagaimana mengenali / menandai / menentukan outline bentuk benda yang berada pada suatu gambar.
Dan salah satu metode paling awal yang didesain untuk memecahkan problem tersebut adalah Active Contour Model yang juga dikenal dengan Snakes (Kaas et al. IJCV1988).
Snakes telah banyak diaplikasikan untuk kebutuhan object tracking, segmentation, edge detection, stereo matching, dan sebagainya.

Gambar 1. Active Contour Model/Snakes (sumber: https://en.wikipedia.org/wiki/Active_contour_model)
Snake direpresentasikan dengan kontur yang dapat berubah-ubah bentuk (deformable contour).
Secara matematis, kontur dapat dimodelkan dengan fungsi kontinu yang mengembalikan nilai titik koordinat 2 dimensi
\[\begin{equation}
\label{eq:contour}
\mathbf{v}: \mathbb{S} \rightarrow \mathbb{R}^2, \text{ dimana } \mathbb{S} \subseteq \{ x \in \mathbb{R} | 0 <= x <= 1\}
\end{equation}\]
dengan \(\mathbf{v}[0]\) dan \(\mathbf{v}[1]\) sebagai titik awal dan akhir dari kontur.
Misalkan kita memiliki kontur/Snake awal \(\mathbf{v}^0\) berada pada sebuah data citra 2D (Gambar 1 kiri), algoritma Snake akan menuntun kontur tersebut menuju lokasi tempat terletaknya outline dari suatu benda (Gambar 1 kanan).
Kontur awal dapat diinisialisasi secara acak atau ditentukan oleh user.
Idealnya kontur akhir akan berada tepat pada outline, yang kita nyatakan dengan \(\mathbf{v}^*\).
Cara Kerja
Bagaimana cara kerja algoritma Snake agar dia bisa menuju ke jalan yang benar?
Snake memanfaatkan energy minimization, yaitu kontur $\mathbf{v}$ beradaptasi untuk mencari nilai energi minimum.
Energi dari Snake diformulasikan dengan functional dalam bentuk integral:
\[\begin{equation}
\label{eq:efunc}
J(\mathbf{v}) = \int_{0}^{1} E_{\mathrm{snake}}(\mathbf{v}(s)) ds
\end{equation}\]
dimana $E_{\mathrm{snake}}(\mathbf{v}(s))$ merupakan fungsi energi yang dievaluasi pada saat $s$.
Bentuk fungsi energi $E_{\mathrm{snake}}$ ini menentukan karakteristik/kelakuan dari Snake.
Algorithma Active Contour Model dimodelkan dengan problem optimisasi sebagai berikut:
\[\begin{equation}
\label{eq:opt}
\mathbf{v}^* := \arg \min_{\mathbf{v}} J(\mathbf{v})
\end{equation}\]
Sebelum membahas solusi dari problem optimisasi di atas, kita perlu terlebih dahulu memahami bentuk fungsi energi $E_{\mathrm{snake}}$.
Fungsi Energi
[Kass, 1988] mendekomposisi $E_{\mathrm{snake}}$ menjadi dua bentuk energi, yaitu energi internal ($E_{\mathrm{int}}$) dan energi external ($E_{\mathrm{ext}}$).
\[\begin{equation}
\label{eq:esnake}
E_{\mathrm{snake}}(\mathbf{v}(s)) = E_{\mathrm{int}}(\mathbf{v}(s)) + E_{\mathrm{ext}}(\mathbf{v}(s)).
\end{equation}\]
Secara umum, energi internal merupakan energi yang berasal dari Snake sendiri, sedangkan energi eksternal merupakan energi yang berasal dari luar, dalam hal ini berasal dari citra 2D.
Berikut ini penjelasan detil dari kedua energi tersebut.
Energi internal. Energi internal berperan dalam mengontrol deformasi dari kontur Snakes. Kita asumsikan fungsi kontur \(\mathbf{v}(s)\) memiliki turunan hingga orde ke-2. Energi internal dinyatakan dalam bentuk penjumlahan turunan pertama dan turunan kedua sebagai berikut:
\[\begin{equation}
E_{\mathrm{int}}(\mathbf{v}(s)) = \frac{1} {2} \left(
\alpha \left\| \frac{ \partial \mathbf{v}(s) } { \partial s } \right\|^2 +
\beta \left\| \frac{ \partial^2 \mathbf{v}(s) } { \partial s^2 } \right\|^2
\right),
\end{equation}\]
dimana konstanta $\alpha$ mengatur tension dan $\beta$ mengontrol rigidigity dari Snake.
Semakin besar nilai $\alpha$, Snake akan tampak seperti garis lurus, yang berarti tidak bersifat seperti ular lagi.
Semakin besar nilai $\beta$ akan membuat Snake semakin tidak lentur.
Nilai $\alpha$ dan $\beta$ harus disetel secara tepat agar Snake deformable, namun disaat yang bersamaan harus tetap menjaga strukturnya sehingga tidak tampak seperti benang kusut.
Energi eksternal. Energi eksternal menentukan ke arah mana Snake harus bergerak untuk mencapai posisi stasioner.
Kita dapat membayangkan semacam ada kekuatan dari luar yang menarik/mendorong Snake untuk menuju posisi tertentu.
Kekuatan dari luar tidak lain berasal dari lingkungan tempat Snake bersemayam, yaitu data citra.
Ada beberapa opsi untuk memodelkan kekuatan dari luar ini, antara lain:
\[\begin{equation*}
E^{(1)}_{\mathrm{ext}} (\mathbf{v}(s)) = | I(s) | \\
E^{(2)}_{\mathrm{ext}} (\mathbf{v}(s)) = -| \nabla I(s) | \\
\end{equation*}\]
$E^{(1)}$ menggunakan langsung piksel dari citra sebagai sumber energi eksternal, sedangkan $E^{(2)}$ menggunakan nilai negatif dari gradient citra.
Terkadang kita perlu untuk mem-blur data citra sedikit sehingga energi akan terdistribusi menjangkau area yang lebih luas.
Ini diperlukan terutama pada situasi dimana Snake diinisialisasi pada posisi yang agak jauh dari target.
Kita dapat memanfaatkan Gaussian filter untuk mem-blur piksel sehingga menghasilkan opsi energi eksternal yang lain
\[\begin{equation*}
E^{(3)}_{\mathrm{ext}} (\mathbf{v}(s)) = | G_{\sigma}(s) \ast I(s) | \\
E^{(4)}_{\mathrm{ext}} (\mathbf{v}(s)) = -|G_{\sigma}(s) \ast \nabla I(s) |,
\end{equation*}\]
atau bahkan menggabungkan raw pixels dengan gradient seperti di bawah ini:
\[\begin{equation*}
E^{(5)}_{\mathrm{ext}} (\mathbf{v}(s) )= w_{\mathrm{line}} | I(s) | + w_{\mathrm{edge}} | \nabla I(s) |
\end{equation*}\]
Solusi Numeris
Sekarang kita akan mencari solusi problem optimisasi Snakes ($\ref{eq:opt}$).
Pertama-tama kita dapat tulis persamaan functional $J(\mathbf{v})$ ($\ref{eq:efunc}$) menjadi
\[\begin{equation}
\label{eq:efunc2}
J(\mathbf{v}) = \int_{0}^{1} E_{\mathrm{snake}}(s, \mathbf{v}(s), \frac{\partial \mathbf{v}}{\partial s}(s), \frac{\partial^2 \mathbf{v}}{\partial s^2}(s)) ds
\end{equation}\]
Penulisan $E_{\mathrm{snake}}$ dengan 4 buah parameter ini dideduksi dari pengetahuan sebelumnya mengenai energi internal dan energi eksternal.
Untuk menyederhanakan notasi, kita tulis $\mathbf{v}^\prime = \frac{ \partial \mathbf{v} }{ \partial s}$ dan $\mathbf{v}^{\prime\prime} = \frac{ \partial^2 \mathbf{v} }{ \partial s^2}$.
Bagaimana mencari fungsi optimum $\mathbf{v}$ dari functional $J(\mathbf{v})$?
Kita akan meminjam teknik dasar dari calculus of variation yang dikenal dengan Euler-Lagrange equation.
Dengan demikian, Euler-Lagrange equation dari persamaan ($\ref{eq:efunc2}$) adalah sebagai berikut:
\[\begin{equation}
\label{eq:euler}
\frac{ \partial }{ \partial \mathbf{v} } E_{\mathrm{snake}} ( s, \mathbf{v}(s), \mathbf{v}^{\prime}(s), \mathbf{v}^{\prime\prime}(s) ) -
\frac{ \partial }{ \partial s \partial \mathbf{v}^{\prime} } E_{\mathrm{snake}} ( s, \mathbf{v}(s), \mathbf{v}^{\prime}(s), \mathbf{v}^{\prime\prime}(s) ) \\
+ \frac{ \partial }{ \partial s^2 \partial \mathbf{v}^{\prime\prime}} E_{\mathrm{snake}} ( s, \mathbf{v}(s), \mathbf{v}^{\prime}(s), \mathbf{v}^{\prime\prime}(s) ) = 0.
\end{equation}\]
Dari pengetahuan kita sebelumnya tentang energi internal dan eksternal, persamaan ($\ref{eq:euler}$) dapat ditulis sebagai berikut:
\[\begin{equation}
\label{eq:euler2}
-F(\mathbf{v}(s)) - \alpha \mathbf{v}^{\prime\prime}(s) + \beta \mathbf{v}^{\prime\prime\prime\prime}(s) = 0
\end{equation}\]
dimana $F(\mathbf{v}) = - \frac{ \partial E_{\mathrm{ext} } (\mathbf{v}) }{ \partial \mathbf{v} }$, yang dapat diinterpretasi sebagai gaya eksternal yang mengarahkan Snake ke lokasi yang memiliki energi minimum.
Secara teori, persamaan ($\ref{eq:euler2}$) dapat diselesaikan secara analitis apabila bentuk fungsi $F(\mathbf{v})$, $\mathbf{v}^\prime$, dan $\mathbf{v}^{\prime\prime}$ diketahui secara pasti.
Namun pada kenyataannya tidak demikian.
Satu-satunya cara yang dapat dilakukan adalah dengan melakukan aproksimasi: mencari solusi $\mathbf{v}^*$ yang mendekati persamaan ($\ref{eq:euler2}$).
Kita akan memanfaatkan finite difference dan solusi iteratif untuk melakukan aproksimasi.
Finite difference.
Finite difference bekerja pada ranah diskrit.
Oleh karena itu, pertama-tama kita nyatakan kontur Snake ($\ref{eq:contour}$) secara diskrit, yaitu sebagai himpunan titik 2D sebagai berikut:
\[\begin{equation}
V = \{ \mathbf{v}_1, \ldots, \mathbf{v}_n \}, \text{ dimana } \mathbf{v}_i = [x_i, y_i]^\top
\end{equation}\]
Masing-masing komponen x dan y dari titik-titik tersebut juga dapat dinyatakan dengan vektor:
\[\begin{eqnarray}
\mathbf{x} &=& [x_1, \ldots, x_n]^\top, \nonumber \\
\label{eq:vaxes}
\mathbf{y} &=& [y_1, \ldots, y_n]^\top.
\end{eqnarray}\]
Finite difference menyatakan bahwa turunan pertama dari fungsi kontur dapat diaproksimasi secara diskrit sebagai berikut:
\[\begin{equation}
\nonumber
\mathbf{v}^{\prime}_{i} \approx \frac{ \mathbf{v}_{i + \frac{1}{2}h} -\mathbf{v}_{i - \frac{1}{2}h} } { h }
\end{equation}\]
Dari sini kita dapat menurunkan persamaan aproksimasi untuk turunan kedua dan keempat, dengan $h=1$:
\[\begin{eqnarray}
\mathbf{v}^{\prime\prime}_{i} &\approx& \mathbf{v}_{i+1} - 2 \mathbf{v}_i+ \mathbf{v}_{i-1} , \nonumber \\
\label{eq:fda}
\mathbf{v}^{\prime\prime\prime\prime}_{i} & \approx & \mathbf{v}_{i+2} - 4 \mathbf{v}_{i+1} + 6\mathbf{v}_i
- 4 \mathbf{v}_{i-1} + \mathbf{v}_{i-2}.
\end{eqnarray}\]
Dengan menggunakan salah satu vektor axis dari kontur $V$ (lihat persamaan ($\ref{eq:vaxes}$)) kita dapat menyatakan persaman ($\ref{eq:fda}$) dalam bentuk matriks dan vektor
\(\begin{eqnarray}
\mathbf{x}^{\prime\prime} & \approx & \mathbf{A} \mathbf{x}, \nonumber \\
\label{eq:fda2}
\mathbf{x}^{\prime\prime\prime\prime} & \approx & \mathbf{B} \mathbf{x},
\end{eqnarray}\)
dimana $\mathbf{A}$ dan $\mathbf{B}$ merupakan pentadiagonal matriks dengan bentuk sebagai berikut:
\[\begin{eqnarray}
\mathbf{A} =
\begin{pmatrix}
-2 & 1 & 0 & 0 & \cdots & 0 & 0 & 1 \\
1 & -2 & 1 & 0 & \cdots & 0 & 0 & 0 \\
0 & 1 & -2 & 1 & \cdots & 0 & 0 & 0 \\
\vdots & \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\
0 & 0 & 0 & 0 & \cdots & 1 & -2 & 1 \\
1 & 0 & 0 & 0 & \cdots & 0 & 1 & -2
\end{pmatrix}, \nonumber\\
\mathbf{B} =
\begin{pmatrix}
6 & -4 & 1 & 0 & \cdots & 0 & 1 & -4 \\
-4 & 6 & -4 & 1 & \cdots & 0 & 0 & 1 \\
1 & -4 & 6 & -4 & \cdots & 0 & 0 & 0 \\
\vdots & \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & \vdots \\
1 & 0 & 0 & 0 & \cdots & -4 & 6 & -4 \\
-4 & 1 & 0 & 0 & \cdots & 1 & -4 & 6
\end{pmatrix}. \nonumber
\end{eqnarray}\]
Hal yang sama juga mesti dilakukan terhadap vektor axis $\mathbf{y}$.
Dengan menggunakan aproksimasi ($\ref{eq:fda2}$) kita dapat menulis ulang persamaan ($\ref{eq:euler2}$) dalam bentuk diskrit untuk masing-masing axis $\mathbf{x}$ and $\mathbf{y}$
\[\begin{eqnarray}
-\mathbf{f}_x - \alpha \mathbf{A} \mathbf{x} + \beta \mathbf{B} \mathbf{x} =
-\mathbf{f}_x + \mathbf{Z} \mathbf{x}= 0, \nonumber \\
\label{eq:euler3}
-\mathbf{f}_y - \alpha \mathbf{A} \mathbf{y} + \beta \mathbf{B} \mathbf{y} =
-\mathbf{f}_y + \mathbf{Z} \mathbf{y} = 0,
\end{eqnarray}\]
dimana $\mathbf{f}_x$ dan $\mathbf{f}_y$ merupakan bentuk diskrit dari $F(\mathbf{v})$ untuk masing-masing axis, dan $\mathbf{Z} = -\alpha \mathbf{A} + \beta \mathbf{B}$.
Perhatikan bahwa solusi untuk $\mathbf{x}$ dan $\mathbf{y}$ dapat diselesaikan secara analitis jika matriks $\mathbf{Z}$ memiliki inverse.
Namun demikian dikarenakan problem optimisasi ($\ref{eq:efunc2}$) non-convex dan non-linear, kita tidak dapat menjamin bahwa solusi analitis memberikan solusi yang cukup baik.
Ditambah lagi dalam kebanyakan aplikasi, kontur awal ditentukan oleh user dan kita menginginkan solusi/kontur akhir tidak jauh dari kontur awal.
Solusi analitis tidak mampu melakukan hal tersebut.
Solusi iteratif.
Untuk mengatasi permasalahan di atas, kita memerlukan mekanisme iteratif yang mengubah kontur awal menjadi kontur akhir yang diinginkan.
Trik yang dapat digunakan adalah dengan mengubah persamaan ($\ref{eq:euler3}$) menjadi dinamis terhadap waktu: memasukkan variabel waktu $t$ dan turunan pertama kontur terhadap waktu $\frac{ \partial \mathbf{x} }{ \partial t}, \frac{ \partial \mathbf{y} }{ \partial t}$
\(\begin{eqnarray}
-\mathbf{f}_{x(t-1)} + \mathbf{Z} \mathbf{x}(t) = - \frac{ \partial \mathbf{x}(t) }{ \partial t } \rightarrow 0 , \nonumber \\
\label{eq:euler4}
-\mathbf{f}_{y(t-1)} + \mathbf{Z} \mathbf{y}(t) = - \frac{ \partial \mathbf{y}(t) }{ \partial t } \rightarrow 0
\end{eqnarray}\)
Makna intuitif dari persamaan di atas adalah bahwa $\mathbf{x}(t)$ dan $\mathbf{y}(t)$ merupakan solusi akhir apabila sama (atau sangat dekat) dengan $\mathbf{x}(t-1)$ dan $\mathbf{y}(t-1)$.
Tanda negatif pada turunan pertama bertujuan untuk menjamin nilai ruas kanan selalu positif karena persyaratan $\mathbf{x}(t) \leq \mathbf{x}(t-1)$.
Dikarenakan turunan pertama $\frac{ \partial \mathbf{x} }{ \partial t}, \frac{ \partial \mathbf{y} }{ \partial t}$ tidak dapat dihitung secara langsung, kita akan gunakan kembali finite difference sehingga menghasilkan persamaan sebagai berikut
\(\begin{eqnarray}
-\mathbf{f}_{x(t-1)} + \mathbf{Z} \mathbf{x}(t) = - \frac{ (\mathbf{x}(t) - \mathbf{x}(t-1) )}{ \tau }, \nonumber \\
\label{eq:euler5}
-\mathbf{f}_{y(t-1)} + \mathbf{Z} \mathbf{y}(t) = - \frac{ (\mathbf{y}(t) - \mathbf{y}(t-1) )}{ \tau },
\end{eqnarray}\)
dengan $\tau>0$.
Dengan sedikit operasi aljabar kita akan mendapatkan persamaan akhir solusi iteratif di bawah ini:
\(\begin{eqnarray}
\mathbf{x}(t) = \left(\mathbf{I} + \tau \mathbf{Z} \right)^{-1} \left( \mathbf{x}(t-1) + \tau \mathbf{f}_{x(t-1)} \right), \nonumber \\
\label{eq:final}
\mathbf{y}(t) = \left(\mathbf{I} + \tau \mathbf{Z} \right)^{-1} \left( \mathbf{y}(t-1) + \tau \mathbf{f}_{y(t-1)} \right),
\end{eqnarray}\)
dimana $\mathbf{I}$ merupakan matriks identitas.
Komputasi persamaan di atas dilakukan berulang-ulang hingga tidak terjadi perubahan terhadap kontur $\mathbf{v}(t) = (\mathbf{x}(t), \mathbf{y}(t))$.
Secara rinci, algoritma Snakes/Active Contour Model dapat ditulis dalam pseudo-code di bawah ini:

Implementasi: Segmentasi Bibir
Kita akan lihat bagaimana performa algoritma Snakes yang telah dijelaskan di atas dalam melakukan segmentasi bibir.
Berikut ini merupakan source code kelas Snakes yang diimplementasi dalam Python.
class Snakes(object):
def __init__(self, name='snakes'):
self.name = name
self.hist = {}
def fit_kaas(self, Im, init_snake, alpha=0.01, beta=0.1,
w_line=0, w_edge=1, tau=100,
bc='periodic', max_px_move=1.0,
max_iter=2500, convergence=0.1, convergence_order=10):
"""
Snake fitting based on the original method
Kaas, M., Witkin, A., Terzopoulos, D. "Snakes: Active Contour Models". [IJCV 1998]
Adopted from skimage active_contour
https://github.com/scikit-image/scikit-image/blob/master/skimage/segmentation/active_contour_model.py
Args:
Im (ndarray) : (H x W) grayscaled image
init_snake (ndarray) : (n, 2) initial snake contour
For periodic snakes, it should not include duplicate endpoints
alpha (float) : Snake length shape parameter
beta (float) : Snake smoothness shape parameter
w_line (float) : Controls attraction to brightness. Use negative values to attract to dark regions
w_edge (float) : Controls attraction to edges. Use negative values to repel snake from edges
tau (float) : time step
bc {'periodic', 'free', 'fixed'} : Boundary conditions for snake. 'periodic' attaches the two ends of the snake
max_px_move : maximum pixel distance to move per iteration
max_iter : maximum iterations to optimize snake shape
convergence : convergence criteria
Returns:
snake (ndarray) : (n, 2) final snake contour
Edge (ndarray) : (H x W) sobel edge image
Map (ndarray) : (H x W) external energy
"""
# Gaussian smoothing
Img = img_as_float(Im)
Img = gaussian(Img, 2)
# Compute edge
Edge = sobel(Img)
# Superimpose intensity and edge images
Img = iproc.normalizeRange(Img, minVal=0, maxVal=1) # normalize to 0-1 values, IMPORTANT!
Edge = iproc.normalizeRange(Edge, minVal=0, maxVal=1)
Map = w_line * Img + w_edge * Edge
# Interpolate for smoothness
intp_fn = RectBivariateSpline(
np.arange(Map.shape[1]),
np.arange(Map.shape[0]),
Map.T, kx=2, ky=2, s=0
)
# Get snake contour axes
x0, y0 = init_snake[:, 0].astype(np.float), init_snake[:, 1].astype(np.float)
# store snake progress
sn = np.array([x0, y0]).T
self.hist['snakes'] = []
self.hist['snakes'].append(sn)
# for convergence computation
xsave = np.empty((convergence_order, len(x0)))
ysave = np.empty((convergence_order, len(y0)))
# Build finite difference matrices
n = len(x0)
A = np.roll(np.eye(n), -1, axis=0) + \
np.roll(np.eye(n), -1, axis=1) - \
2*np.eye(n) # second order derivative, central difference
B = np.roll(np.eye(n), -2, axis=0) + \
np.roll(np.eye(n), -2, axis=1) - \
4*np.roll(np.eye(n), -1, axis=0) - \
4*np.roll(np.eye(n), -1, axis=1) + \
6*np.eye(n) # fourth order derivative, central difference
Z = -alpha*A + beta*B
# Impose boundary conditions different from periodic:
sfixed = False
if bc.startswith('fixed'):
Z[0, :] = 0
Z[1, :] = 0
Z[1, :3] = [1, -2, 1]
sfixed = True
efixed = False
if bc.endswith('fixed'):
Z[-1, :] = 0
Z[-2, :] = 0
Z[-2, -3:] = [1, -2, 1]
efixed = True
sfree = False
if bc.startswith('free'):
Z[0, :] = 0
Z[0, :3] = [1, -2, 1]
Z[1, :] = 0
Z[1, :4] = [-1, 3, -3, 1]
sfree = True
efree = False
if bc.endswith('free'):
Z[-1, :] = 0
Z[-1, -3:] = [1, -2, 1]
Z[-2, :] = 0
Z[-2, -4:] = [-1, 3, -3, 1]
efree = True
# Calculate inverse
Zinv = scipy.linalg.inv(np.eye(n) + tau * Z)
# Snake energy minimization
x = np.copy(x0)
y = np.copy(y0)
for i in range(max_iter):
fx = intp_fn(x, y, dx=1, grid=False)
fy = intp_fn(x, y, dy=1, grid=False)
if sfixed:
fx[0] = 0
fx[0] = 0
if efixed:
fx[-1] = 0
fy[-1] = 0
if sfree:
fx[0] *= 2
fy[0] *= 2
if efree:
fx[-1] *= 2
fy[-1] *= 2
xn = np.dot(Zinv, x + tau * fx)
yn = np.dot(Zinv, y + tau * fy)
# Movements are capped to max_px_move per iter
dx = max_px_move * np.tanh(xn-x)
dy = max_px_move * np.tanh(yn-y)
if sfixed:
dx[0] = 0
dy[0] = 0
if efixed:
dx[-1] = 0
dy[-1] = 0
x += dx
y += dy
# Convergence criteria
# - x(t) - x(t-i} < convergence
# - i: the last k (convergence_order) of previous snakes
j = i % (convergence_order+1)
dist = 10000000
if j < convergence_order:
xsave[j, :] = x
ysave[j, :] = y
else:
dist = np.min(np.max(np.abs(xsave-x[None, :]) +
np.abs(ysave-y[None, :]), 1))
if dist < convergence:
break
print('Iter-%d/%d: convergence_order: %d, j: %d, dist: %f' % (i, max_iter, convergence_order, j, dist))
# store snake progress
sn = np.array([x, y]).T
self.hist['snakes'].append(sn)
# end for
snake = np.array([x, y]).T
return snake, Edge, Map, Img
Fungsi utama dari kode di atas adalah $\text{fit_kaas(.)}$ yang menjalankan algoritma iteratif Snakes.
Ada beberapa hal teknis yang perlu diperhatikan yaitu:
- Edge image dihasilkan dengan sobel image detector yang digunakan sebagai energi eksternal. Energi eksternal bisa berupa kombinasi antara gambar asli dengan gambar edge dengan memainkan parameter $w_{\mathrm{line}}$ dan $w_{\mathrm{edge}}$.
- Turunan pertama energi eksternal dari Snakes ($\mathbf{f}_x, \mathbf{f}_y$) didapatkan dengan menggunakan RectBivariateSpline
- Kriteria untuk memberhentikan iterasi algoritma Snakes dilakukan dengan membandingkan kontur terakhir dengan 10 kontur sebelumnya
Gambar-gambar berikut ini merupakan hasil segmentasi bibir dari algoritma Snakes.
Kontur awal berbentuk elips yang dibuat secara manual. Lalu algoritma Snakes mengarahkan elips tersebut agar merekat di bibir bagian luar.

(a) Original |

(b) Gaussian smoothed |

(c) External energy (edge) |
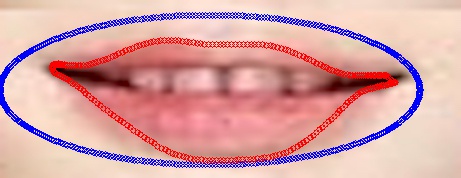
(d) Snakes |
Gambar 2. Segmentasi bibir dengan Snakes. Gambar (a) merupakan gambar asli; (b) merupakan gambar grayscale dari (a) dan juga dihaluskan dengan Gaussian filter;
(c) merupakan gambar edge hasil dari operasi sobel; (d) menampilkan kontur awal (biru) dan kontur akhir (merah) hasil algoritma Snakes.
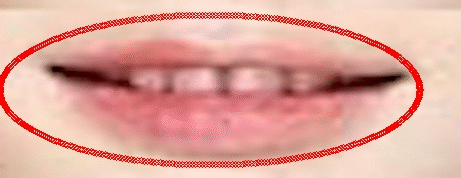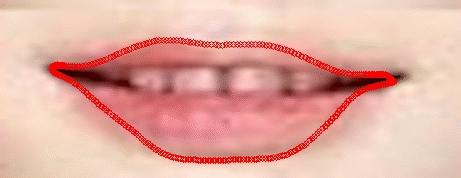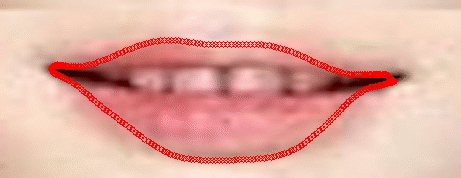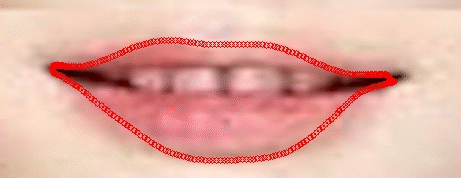
Gambar 3. Progres deformasi dari kontur Snakes (54 iterasi)
Untuk mengetahui teknis yang lebih lengkap lagi dan menghasilkan gambar-gambar di atas dapat mengakses ke code repository https://github.com/ghif/ActiveContourModel.